Beispiel: Zahlentheorie

Die Schritte "Probleme erkennen", "Ursachen untersuchen" und "Ziele definieren" spielen zunächst keine Rolle, wir beschäftigen uns also mit dem Schritt "Lösungen entwickeln". Dazu benutzen wir in der Map die Abkürzung "le". Solche Kürzel können sehr dabei helfen, strukturiert vorzugehen.
Hier kommt die Werkzeug-Map "Lösungen entwickeln":

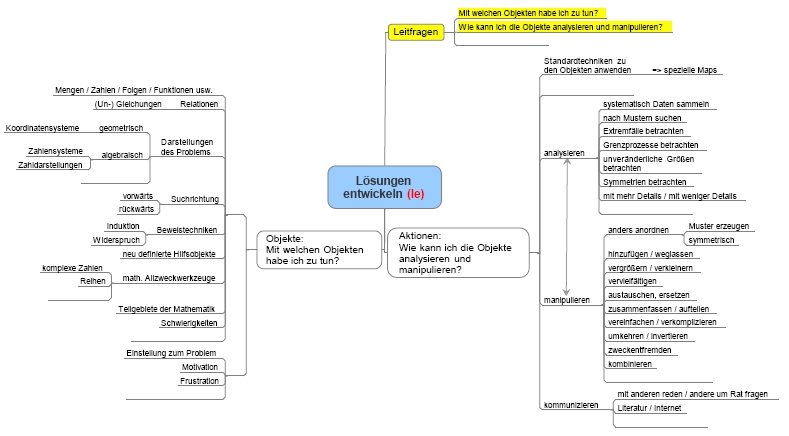
Wir sammeln ein paar aussichtsreiche Ideen:
Spezialfälle betrachten, einen Widerspruchsbeweis führen, verschiedene Darstellungen des Problems sammeln.
Wir untersuchen zunächst Spezialfälle und legen die kleine Übersicht unter Punkt 1 an.
Das führt zu der Einsicht, dass Primzahlen keine Kandidaten für unser Problem sind.
Im Übrigen scheinen die Spezialfälle aber nicht sehr ergiebig.
Wir wenden uns deshalb als nächstes verschiedenen Darstellungen des Problems zu - dies scheint uns günstiger als der Versuch, einen Widerspruchsbeweis zu konstruieren.
Eine algebraische Darstellung scheint aussichtsreicher als eine grafische.
Unter Punkt 2 betrachten wir n = m² + p und stellen diese Gleichung um.
Die Gleichung p = n - m² scheint besonders interessant.
Was ist eigentlich in dieser Darstellung das Ziel?
Um das herauszubekommen, notieren wir "zd" = "Ziele definieren" und markieren das mit einem Kontrollkästchen "[ ]".
Dieses Kontrollkästchen dient später der Prüfung, ob wir das genannte Ziel tatsächlich erreicht haben.
Details zum Schritt "Ziel definieren" beschreiben wir unter Punkt 3:
Wir wollen n so bestimmen, dass n - m² zusammengesetzt ist für alle n und m mit m² < n.
Mit dem Werkzeug "le" suchen wir nun nach Lösungsansätzen zu diesem Ziel.
Dabei können wir die Werkzeug-Map zur Zahlentheorie benutzen:

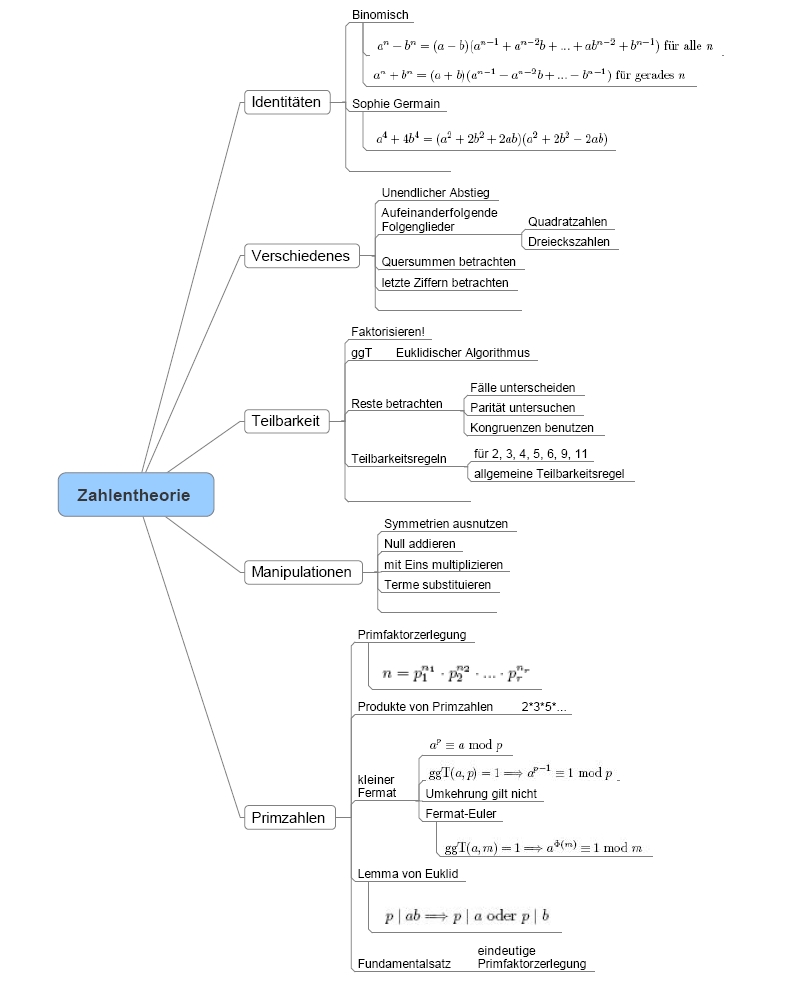
Wir wollen die Differenz n - m² auf Zusammengesetztheit untersuchen. Da liegt der dritte binomische Lehrsatz nahe: Setze n = k² und benutze
k² - m² = (k-m )(k+m).
Mit dieser Idee laufen die Dinge zunächst wie von selbst.
Allerdings stoßen wir auf eine Schwierigkeit: Die Zerlegung mit dem binomischen Satz garantiert nicht, dass n - m² = k² - m² zusammengesetzt ist.
Um uns erste Rechenschaft abzulegen über den problematischen Fall m = k - 1 benutzen wir das Werkzeug "ab" = "Abstand gewinnen".
Zum Schluss machen wir einen Rückblick und benutzen das Kürzel "rb". Dabei erinnert uns das Kontrollkästchen [ ] an die Prüfung, ob wir das gesetzte Ziel erreicht haben.
Außerdem kontrollieren wir unsere Lösung unter Punkt 7 - und stoßen schließlich auf weitergehende Fragen, die wir als nächstes untersuchen können.

Wer weiterlesen möchte: Es folgen vermischte Ideen zum Problemlösen. [mehr...]