Problemlösen: Grundideen

Die Grundidee
Probleme löst man am besten, indem man passende "Lösungswerkzeuge" benutzt.
Hier kommen einige wenige Beispiele für solche Werkzeuge:
- Spezialfälle betrachten,
- eine Skizze anfertigen,
- eine vollständige Induktion durchführen,
- mit dem Ziel beginnen und rückwärts suchen,
- Extremfälle betrachten,
- nach Symmetrien suchen,
- den Satz des Pythagoras benutzen oder
- eine Definition nachschlagen.

All diese Werkzeuge können uns beim Lösen eines Problems weiterbringen.
Die Menge solcher Werkzeuge ist natürlich riesig, und eine bloße Sammlung hilft nur wenig - wir brauchen eine Antwort auf die
Zentrale Frage beim Problemlösen
In welcher Problemsituation hilft welches Werkzeug?

Diese Frage zerlegen wir in zwei Teilfragen:

Teilfrage 1: Welche Problemsituationen sind wichtig?
Probleme sind vielfältig, und wir können nicht für jede denkbare Bearbeitungssituation ein eigenes, passendes Werkzeug bereit halten.
Deshalb werden wir Problemsituationen geschickt klassifizieren.
Beispiele sind die folgenden Klassifikationen:
nach Problemphasen:
- Orientierung zu Beginn der Bearbeitung,
- Planung des Lösungswegs,
- Durchführung der Lösung,
- Rückschau
nach den mathematischen Objekten, mit denen das Problem zu tun hat
- Reihen,
- Matrizen,
- differenzierbare Funktionen
oder
nach typischen Schwierigkeiten, die beim Problemlösen auftauchen
- keinen Anfang wissen,
- feststecken,
- den Überblick verlieren...

Teilfrage 2: Welche Werkzeuge helfen in den Problemsituationen aus Teilfrage 1?
Eine solche Zuordnung "Problemsituationen - > Werkzeuge" ist ein grundlegender Teil unserer Lösungsmethode.
Hier sind ein paar einfache Beispiele für solche Zuordnungen:
- Oft empfiehlt es sich, zu Beginn der Bearbeitung eine Zeichnung anzufertigen.
- Wenn die Ausgangsinformationen nicht viel hergeben, kann man versuchen, vom Ziel her rückwärts zu arbeiten.
- Beim Umgang mit Folgen von Zahlen sind induktive Schlüsse von einer Zahl auf ihre Nachbarn oft nützlich.
Problemsituationen und Werkzeuge: Ordnung schaffen mit Mind Maps
Diese Zuordnung "Problemsituationen - >Werkzeuge" soll nicht nur im Kopf stattfinden, sondern auch schriftlich erfasst werden - dann nämlich lassen sich Werkzeuge viel zuverlässiger und systematischer benutzen.
Wir benötigen also eine Methode, um diese Zuordnung schriftlich darzustellen.
Dafür besonders geeignet ist das Mind Mapping.

Mind Mapping: Wie funktioniert das?
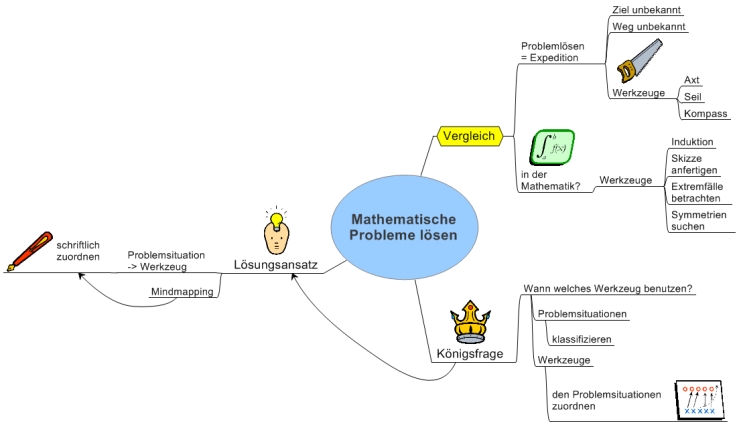
Beim Mind Mapping wird das Thema in die Mitte des Schreibblatts geschrieben, die Ideen werden hierarchisch um das Thema herum angeordnet und zeichnerisch dargestellt, sofern das sinnvoll ist.
Hier kommt ein Beispiel.
(Es war einfacher, eine Mind Map mit dem Computer zu erzeugen, als eine handschriftliche einzuscannen.)

Mind Maps: Flexibel und leistungsfähig
Wir können nämlich Mind Maps auf zwei Arten benutzen:

1. Als "Werkzeug-Map"
Hier ordnen wir den Problemsituationen Werkzeuge so zu, dass sich ein passendes Werkzeug leicht finden lässt.

2. Als "Problem-Map"
In dieser Map bearbeiten wir das eigentliche Problem - wir sammeln und entwickeln Ansätze, zerlegen das Problem in Teilprobleme, notieren spontane Ideen usw., und benutzen die Werkzeug-Maps, wenn wir Ideen zu neuen Lösungswerkzeuge brauchen.

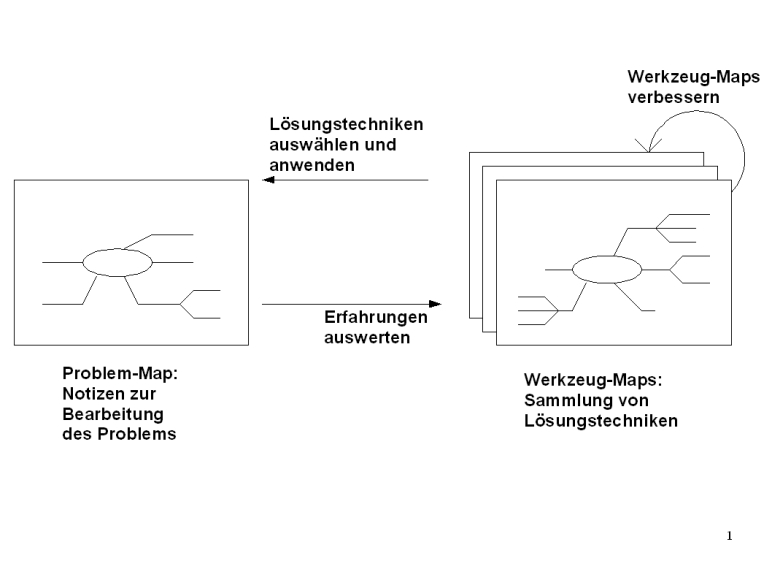
Dieser kombinierte Einsatz von Werkzeug- und Problem- Maps bekommt der Kürze halber den Namen "Werkzeug- Mapping".

So funktioniert Werkzeug-Mapping:

Das klingt umständlich oder unnötig kompliziert?

Mag sein. Aber es gilt vor allem: Das Verfahren ist alltagstauglich, Werkzeug- Maps helfen beim systematischen Einsatz von Lösungswerkzeugen und Problem- Maps bringen Struktur in die Suche nach einer Lösung.
(Mehr zur Kritik am Werkzeug-Mapping und zu den Entgegnungen darauf gibt es hier.)

Nach diesem Überblick kommen wir jetzt zu den Einzelheiten.
Wir beginnen mit der Frage:
Wie funktioniert Mind Mapping? [mehr...]
Wer das Mind Mapping schon kennt, kann weitermachen mit der Frage:
Wie helfen Mind Maps beim Lösen mathematischer Probleme?[mehr...]

Seitenanfang