Ein Lösungsverfahren

eine Problem-Map:
Hier planen wir unser Vorgehen, sammeln Ideen, verfolgen Ansätze, untersuchen systematisch Schwierigkeiten etc., und
eine (oder mehrere) Werkzeug- Maps:
Hier haben wir Lösungswerkzeuge gesammelt und so aufbereitet, dass wir möglichst leicht ein passendes finden.
Diese Werkzeug-Maps bilden unseren "Werkzeug- Koffer", sie speichern unsere Erfahrungen aus früheren Problemen und können immer weiter verbessert werden.

Diese Maps werden wir jetzt genauer untersuchen.

Wie können Problem-Maps beim Problemlösen helfen?

In Problem-Maps können wir

Ziele sammeln, ein vielsprechendes Ziel auswählen und weiter verfolgen,
Lösungsansätze sammeln, den meistversprechenden auswählen und weiter verfolgen,
ein Problem in Teilprobleme zerlegen,
einen Plan für das Vorgehen entwerfen,
das Vorgehen kritisch untersuchen und anpassen,
Schwierigkeiten ausfindig machen und nach Lösungen suchen usw.

Keine Sorge! Niemand will das Problemlösen in ein Korsett zwängen: Problem-Maps sollen beim Nachdenken helfen, und dabei spielt Intuition eine große Rolle - zu viele Regeln sind hier bloß schädlich. Wenn es der Lösung eines Problems dient, darf und soll natürlich jeder Ratschlag auf diesen Seiten verletzt werden.
Aber gerade dann, wenn man in Schwierigkeiten steckt, ist es oft sehr nützlich, systematischer zu arbeiten.

Beim Lösen mathematischer Probleme in Mind Maps gibt es eine praktische Schwierigkeit: Immer wieder braucht man Tabellen, Termumformungen, Nebenrechnungen - all das passt nur schlecht ins klassische Layout einer Mind Map.

Deshalb mein Vorschlag:

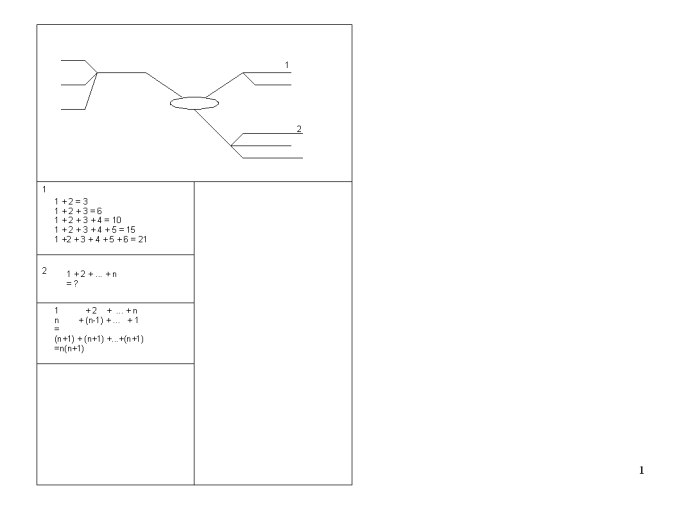
Ein Misch-Layout für die Problem-Map

Bei dieser Aufteilung sammelt man Ideen in der Mind Map, Nebenrechnungen und Termumformungen werden in den Kästchen unter der Map ausgeführt, einfache Ziffern verweisen von der Map auf die Kästchen. Die Mittellinie zwischen den Kästchen hilft beim Platzsparen und sorgt für mehr Übersichtlichkeit.
(Die Idee zur Aufteilung in Kästchen stammt aus einem Aufsatz von Richard Rusczyk auf der Seite "www.artofproblemsolving.com".)

Beispiele solcher Problem-Maps betrachten wir später.

Wie können Werkzeug-Maps beim Problemlösen helfen?

Wir brauchen einen Weg, um in schwierigen Problemsituationen diejenigen Werkzeuge ausfindig zu machen, die uns weiterhelfen.
Dazu gehen wir folgendermaßen vor:
1. Wir klassifizieren Problemsituationen.
2. Wir ordnen diesen Problemsituationen nützliche Werkzeuge zu.

Wir wollen zunächst untersuchen, wie das grundsätzlich aussehen könnte.
Im nächsten Kapitel gibt es dann eine Sammlung von Werkzeug-Maps für den praktischen Einsatz.

Wie lassen sich Problemsituationen klassifizieren?
Dies gelingt am einfachsten mit Hilfe von Dingen, die sich leicht feststellen lassen:

In welcher Phase einer Problembearbeitung stecke ich gerade?
Eine sinnvolle Aufteilung in Phasen sieht zum Beispiel so aus:
- Orientieren,
- Planen,
- Durchführen,
- Rückblicken.
Diese Phasen folgen in der Praxis nicht streng aufeinander, aber es ist meist leicht festzustellen, in welcher Phase man sich gerade befindet.Jeder dieser Phasen kann man nützliche Werkzeuge zuordnen.
In welchen Schwierigkeiten stecke ich gerade?
Die Schwierigkeiten, die beim Problemlösen auftauchen, sind oft sehr individuell.
Beispiele für derartige Schwierigkeiten könnten sein:
Ziellosigkeit,
Mangel an planvollem Vorgehen,
Ungenauigkeit, Flüchtigkeit,
Mangel an Einfällen.
Diesen Unzulänglichkeiten lassen sichWorin besteht das Problem?
Diese Frage soll folgendes bedeuten: Beim Problemlösen kann man eine ganze Reihe von abstrakteren Objekten unterscheiden, zum Beispiel
Ziele,
Lösungsansätze,
Lösungspläne,
Emotionen, die sich auf das Problemlösen beziehen,
Repräsentationen: In welcher Form betrachten wir eigentlich das Problem - mittels Grafiken, durch Formeln, verbal...?
Beim Problemlösen können wir dann untersuchen, welche Schwierigkeiten sich an diese Objekte knüpfen: Fehlen uns Ziele? Sind die bisherigen Lösungsansätze unzureichend? Brauchen wir nicht bloß einen Lösungsansatz, sondern einen umfassenderen Plan?
Dieser Ansatz ist eng verwandt mit der Gliederung nach Schwierigkeiten, die weiter oben beschrieben wurde. wiederum Werkzeuge zuordnen.
Mit welchem Teilgebiet der Mathematik und welchen mathematischen Objekten habe ich zu tun?
Dieser Ansatz ist recht naheliegend: Man sammelt in einer Map Werkzeuge zum Umgang mit
Polynomen,
konvergierenden Reihen,
stochastischen Prozessen usw.

Es ist klar, dass dieser Ansatz im Äußersten auf die Kartographierung des gesamten mathematischen Wissens führen würde - wie sich entsprechende Werkzeug-Maps erstellen oder nutzen ließen, ist völlig unklar. In diesem Ansatz berühren sich Techniken des Problemlösens und die Frage nach der Aufbereitung mathematischen Wissen im Allgemeinen.
Für den praktischen Gebrauch sind allerdings schon kleinere Werkzeug- Maps mit den wichtigsten Werkzeugen sehr nützlich.

Eine Übersicht über die Werkzeug-Maps findet sich hier.

Wie arbeitet man mit Werkzeug-Maps?

Wir unterscheiden drei Vorgänge:

Werkzeug-Maps erstellen
Werkzeug-Maps benutzen
Werkzeug-Maps anpassen

Zu diesen Punkten ein paar Hinweise:

Werkzeug-Maps erstellen:
Beim Erstellen eigener Werkzeug- Maps lässt sich sehr viel lernen über den Vorgang des Problemlösens - wer stattdessen nur vorgefertigte Werkzeug-Maps übernimmt, der bringt sich um diesen großen Vorteil des Werkzeug- Mapping.
Vorgefertigte Werkzeug-Maps wie auf dieser Seite können vor allem Ideen liefern, und zwar
Ideen zu möglichen Gliederungen und damit zu Möglichkeiten, Problemsituationen wahrzunehmen und einzuschätzen, und
Ideen zu möglichen Werkzeugen: So sind zum Beispiel die Betrachtung von Extremfällen oder die Suche nach Invarianten und Symmetrien typische mathematische Werkzeuge, die leichter zu übernehmen als nachzuerfinden sind.
Werkzeug-Maps benutzen:
Während man ein Problem bearbeitet, sollte man sich von den folgenden Extremen fernhalten:
Einerseits: Werkzeuge zu selten einsetzen - zum Beispiel ziellos und unscharf zu denken, obwohl schon einfache Werkzeuge aus einer Werkzeug- Map hier große Verbesserungen bewirken können.
Andererseits: Werkzeuge zu sklavisch einsetzen - zum Beispiel sich zwanghaft an Werkzeug-Maps zu klammern und dadurch den Gedankenfluss zu hemmen.
Werkzeug-Maps anpassen:
Wenn man Werkzeug-Maps anpassen und verbessern will, dann kann man dafür wiederum Werkzeuge benutzen.
(Das klingt arg verkünstelt? Das scheint zunächst vielleicht so, aber es besteht in der Literatur Einigkeit darüber, dass der Rückblick auf die Bearbeitung eines Problems die vielleicht wichtigste und lehrreichste Phase ist.)
Ein Beispiel einer solchen Werkzeug- Map für den Rückblick steht hier.

Wir kommen jetzt zu den Werkzeug- Maps. [mehr ...]

Seitenanfang